Le petit p bidon sous-puissant

Quelques définitions sur les risques

Considérant que la plupart des études font des comparaisons bilatérales, qu’il s’agisse d’épidémiologie ou de recherche clinique, l’hypothèse nulle est généralement l’absence totale d’effet de l’intervention ou l’exposition considérée. La plausibilité de cette hypothèse nulle est généralement douteuse, notamment pour les essais cliniques dans lesquels la question porte plus sur le signe et l’amplitude de l’effet que sur la réalité d’un effet. En bref, il paraît absolument impensable que le traitement médical ou chirurgical de la hernie discale ait exactement le même résultat fonctionnel à 1 an. Quand je dis, exactement le même résultat fonctionnel, c’est que la moyenne d’une échelle fonctionnelle serait identique même avec 10 000 chiffres après la virgule. Les vraies questions qui se posent sont :

1. Lequel des deux traitements est le meilleur (signe de la différence) ?
2. Est-ce que les deux traitements ont un résultat fonctionnel moyen presque équivalent ou très différent ?

Au sens strict, c’est la balance bénéfices/risques qu’on doit évaluer, en prenant en compte les effets indésirables médicamenteux et les complications chirurgicales, mais pour simplifier, on se concentre sur le résultat fonctionnel dans un premier temps.

Considérant donc que les deux traitements ne peuvent pas être strictement équivalents, le risque l’erreur de première espèce n’existe pas, au sens strict, mais elle est remplacée par les deux risques suivants :

1. Conclure à l’existence d’une différence dans le sens opposé de la réalité (erreur de troisième espèce).
2. Conclure à l’existence d’une différence importante alors que la différence réelle est totalement négligeable (quasi-équivalence). J’appellerai ça l’erreur de type Ib.

Définition du petit p bidon sous-puissant

Lorsqu’on utilise un échantillon trop petit et qu’on recherche un effet modeste, alors le signal (effet réel) devient négligeable par rapport au bruit (erreur aléatoire), de telle sorte qu’avec un seuil de significativité bilatéral à 5%, on a 2.5% de chances de conclure à une différence significative dans un sens et 2.5% de chance de conclure à une différence significative dans l’autre sens.

Dans ce contexte, le petit p est indépendant de la différence réelle. Un petit p significatif n’apporte plus aucune information. Il n’aide pas à identifier la réalité d’une différence non négligeable puisqu’il a la même probabilité d’arriver que la différence soit nulle, négligeable, ou non négligeable. Il n’aide pas non plus à identifier la direction de la différence puisqu’il a autant de chances d’aller dans le bon sens que dans le sens opposé et est donc indépendant du signe de la différence et donc non informatif dessus.

Je parlerai donc de petit p bidon sous-puissant pour décrire les petits p significatifs dans une situation de rapport signal/bruit très proche de zéro. Cela regroupe donc, trois cas :

1. La différence réelle est négligeable ou nulle, mais le petit p est significatif
2. La différence réelle n’est pas négligeable mais le petit p va dans le mauvaise direction (erreur de troisième espèce)
3. La différence réelle n’est pas négligeable et le petit p va dans la bonne direction, mais il y avait autant de chances que ça aille dans la direction opposée, de telle sorte, que ce n’est que par pure chance que la conclusion de l’étude est correcte.

Considérer que le troisième item est bidon peut vous choquer, mais cela me paraît pertinent du point de vue de l’information. De mon point de vue, des propos peuvent être considérés de bidon, s’ils sont totalement indépendants de la réalité, ce qui implique de dire parfois des choses vraies et parfois des choses fausses. Quelque chose est bidon à partir du moment où il est décorrélé de la réalité. À l’opposé, dire systématiquement le contraire de la réalité, c’est informatif, puisqu’on peut alors croire le contraire de ce qui est dit.

Sémiologie

Devant un petit p significatif, certains signes évoquent un petit p bidon sous-puissant.

1. Échantillon de toute petite taille face à l’effet attendu, suggérant une puissance très faible
2. Estimation ponctuelle démesurée en comparaison à ce qui paraît plausible
3. Petit p à la limite de la significativité (p typiquement compris entre 0.01 et 0.05)
4. Multiplicité des tests, apparente ou cachée
5. Autres tests répondant à la même question ne montrant pas plus de tendance à la significativité que ce qui est explicable par le hasard (environ un petit p sur 20 significatif, la moitié du temps dans le sens opposé à ce que veulent montrer les auteurs)
6. Lorsqu’une différence d’évolution (p.e. Student inter-groupe sur différences intra-sujets) est analysée sur un paramètre dont la stabilité est attendue, apparition d’une dégradation importante dans le groupe contrôle et d’une amélioration de même amplitude dans le groupe expérimental et une différence à baseline qui va dans le sens opposé à la différence finale.
7. Lorsqu’une différence d’évolution est analysée sur un paramètre qui doit évoluer, la moitié de la différence des différences est due à la différence à baseline et l’autre moitié à la différence finale.

Certains de critères sont très subjectifs, telle que les deux premiers, mais lorsque beaucoup d’éléments sont présent et fortement marqués, le tableau est évocateur.

À un niveau plus global de la littérature, une méta-analyse peut estimer de manière à peu près correcte l’effet réel avec des milliers de patients, ce qui permet ensuite de mieux identifier les études sous-puissantes. On peut craindre un biais de publication ainsi qu’un selective reporting biais dans ces études.

La multiplicité des tests cachée a sa propre sémiologie:

1. Écart au protocole, sur les analyses (suspect lorsque celui-ci est disponible)
2. Critères de jugements présentés dans la partie méthodes mais pas dans les résultats
3. Grande majorité (voire totalité) de petits p significatifs (suggérant une très bonne puissance sur tous les tests réalisés) dans les résultats, mais presque tous compris entre 0.01 et 0.05 (alors qu’en cas de puissance à 90%, on en a 50% de petits p en dessous de 0.0012)
4. Étrangeté des analyses qui « tirent dans les coins », comme la corrélation entre le max d’un dosage biologique entre J1 et J4 corrélé à la mortalité en réa, puis la moyenne d’un autre dosage biologique entre J2 et J3 corrélé à la mortalité intra-hospitalière, tous deux dans le même article.
5. Critère de jugement principal inattendu étant donné la population et l’intervention, voire disparition des critères de jugements attendus.

Explication des critère N°6 et 7

Je crains que la pertinence de ce critère ne paraisse pas être une évidence au novice. Pour le comprendre, il faut raisonner en termes de distributions conditionnelles au petit p significatif. Pour cela, je partirai d’un cas d’école. Nous allons expliquer le critère N°6. Le N°7 est une variante assez simple qui en découle directement.

L’article est intitulé « Special nutrition intervention is required for muscle protective efficacy of physical exercise in elderly people at highest risk of sarcopenia« . La qualité du reporting est bien pourrie, les critères d’inclusion flous, mais on peut comprendre qu’il s’agit d’une population de patients âgés fragiles, avec une sarcopénie mais en état clinique stable. Randomisation de 17 patients (groupe qui bénéfice de kinésithérapie seule) vs 17 patients (groupe qui bénéfice de kinésithérapie + FortiFit). Le FortiFit, est un complément alimentaire à base de protéines de lactosérum et de vitamines. Plusieurs tests standardisés sont passés à baseline et à trois mois. Furent enregistrés par impédancemétrie : la masse muculaire (kg), la masse maigre (kg), l’indice de masse maigre (kg/m²), la force musculaire au handgrip test, le Short Physical Performance Battery divisable lui-même en test d’équilibre, test de vitesse de marche et test de lever de chaise. Cela fait 8 critères de jugement potentiels, assez redondants. Trois méthodes statistiques principales sont aussi possibles pour les comparaisons du résultat à trois mois : test de Student sur les résultats à 3 mois, test de Student sur les changements (3 mois moins baseline), et modèle linéaire expliquant le résultat à 3 mois par le groupe de traitement et le résultat du test à baseline. Cela fait donc 24 analyses statistiques possibles. On ne sait pas trop quelles analyses étaient planifiées étant donné qu’on n’a pas accès au protocole.

Quel est le résultat ?

	Handgrip test Baseline Moyenne ± SEM	Handgrip test 3 mois Moyenne ± SEM	Changement moyen
Groupe contrôle	23.73±2.06 kg	22.18±2.19 kg	-1.55
Groupe FortiFit	22.51±2.35 kg	24.54 ± 2.65 kg	+2.03

Le test de Student des changements (3 mois moins baseline) est significatif (p=0.013), montrant que les sujets améliorent plus leur force musculaire avec le Handgrip test. Il y a une incohérence entre le texte et la figure 1 qui semble montrer seulement une augmentation moyenne de force de +1.6 kg dans le groupe FortiFit. Il y a peut-être un mélange accidentel de données entre les forces et masses musculaires (qui sont proches).

N’y a-t-il rien d’étonnant ? Pourquoi des patients, en état stable, perdent-ils 1.55 kg au handgrip test alors qu’ils bénéficient de kinésithérapie ? Pourquoi la différence entre les groupes à baseline est-elle dans le sens opposé de la différence finale ?

Pour commencer, considérons la distribution des changements moyens (ici, les changements moyens observés sont -1.55 kg et +2.03 kg), conditionnelle à une espérance nulle du changement dans chaque groupe. Sous hypothèse d’homoscédasticité, les deux changements moyens ont la même variance car les groupes sont de taille égale. Ils sont aussi indépendants. Par le théorème central limite, la distribution jointe de ces deux moyennes de changement est donc approximable à une distribution binormale avec une corrélation nulle, centrée autour du point (0,0).

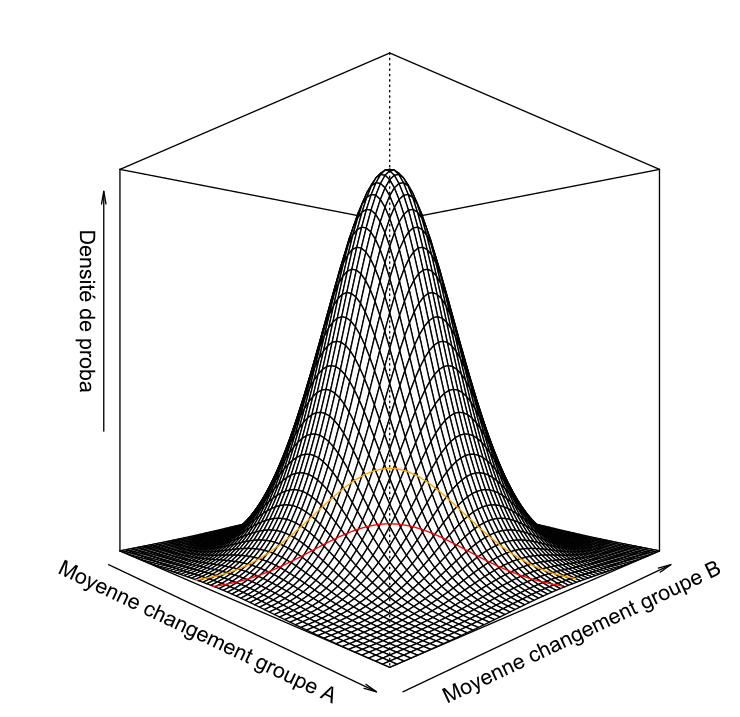
La figure présente la distribution binormale ainsi que le seuil de significativité à 10% bilatéral (orange) et 5% bilatéral (rouge). Conditionnellement à un petit p < 0.05, on constate que la densité de proba bivariée est maximale pour des moyennes égales et de signe opposé. Présenté sous un autre angle, sachant que la différence est de 2 erreurs types entre les deux groupes, il est bien plus probable d’avoir -1 erreur type dans un groupe et +1 erreur type dans l’autre groupe, que +0 erreur type dans un groupe et +2 erreurs types dans l’autre et il est encore plus improbable d’avoir +1 erreur type dans un groupe et +3 erreurs types dans l’autre !

En conditionnant la distribution binormale à un petit p < 0.05, j’ai pu calculer numériquement une probabilité d’avoir un ratio des différences de moyenne compris entre -0.5 et -2. Cette probabilité est estimée à 56%. La probabilité d’un ratio négatif (c’est-à-dire, que les deux changements moyens sont de signe opposé) est estimée à 97.5%.

En réalisant la même considération en analyse tétravariée, on peut calculer que la densité de probabilité maximale est concentrée sur le scenario suivant

	Handgrip test Baseline Moyenne ± SEM	Handgrip test 3 mois Moyenne ± SEM	Changement moyen
Groupe contrôle	µ + epsilon	µ – epsilon	-2×epsilon
Groupe FortiFit	µ – epsilon	µ + epsilon	+2×epsilon

Où µ représente l’espérance commune aux quatre cases et epsilon est la valeur telle que la différence fournisse un p=0.05, c’est-à-dire la plus petite valeur qui conduise à un résultat statistiquement significatif.

Évidemment, le point de densité de probabilité le plus élevé reste infiniment improbable puisque les distributions sont continues. Les quatre écarts à la moyenne générale diffèreront donc plus ou moins, mais les grandes tendances devraient souvent apparaître.

Le cas observé semble donc bien typique, si on présente les différences par rapport à la moyenne générale (quatre cases moyennées) :

	Handgrip test Baseline Moyenne ± SEM	Handgrip test 3 mois Moyenne ± SEM	Changement moyen
Groupe contrôle	m + 0.49	m – 1.06	-1.55
Groupe FortiFit	m – 0.73	m + 1.30	+2.03

Un peu de pratique

Reprenons le cas d’école et appliquons la liste des critères :

1. Échantillon de toute petite taille face à l’effet attendu, suggérant une puissance très faible. CHECK
2. Estimation ponctuelle démesurée en comparaison à ce qui paraît plausible. DISCUTABLE
3. Petit p à la limite de la significativité (p typiquement compris entre 0.01 et 0.05) CHECK
4. Multiplicité des tests, apparente ou cachée CHECK. N=3 tests apparents (avec test complètement inapproprié) seulement, mais nombreux critères de jugements mesurés mais non présentés dans les résultats. Un des tests présentés n’était même pas dans ma liste des tests imaginables et cache un choix de seuillage sur une variable catégorielle ordinale (-> deux tests possibles).
5. Autres tests répondant à la même question ne montrant pas plus de tendance à la significativité que ce qui est explicable par le hasard (environ un petit p sur 20 significatif, la moitié du temps dans le sens opposé à ce que veulent montrer les auteurs). FAILED. Sur les trois tests présentés, deux vont dans le même sens et le troisième n’est pas reproductible mais irait dans le même sens selon les auteurs. Ce FAIL pourrait être dû à la non présentation de nombreux tests cachés.
6. Lorsqu’une différence d’évolution (p.e. Student inter-groupe sur différences intra-sujets) est analysée sur un paramètre dont la stabilité est attendue, apparition d’une dégradation importante dans le groupe contrôle et d’une amélioration de même amplitude dans le groupe expérimental et une différence à baseline qui va dans le sens opposé à la différence finale. CHECK pour le premier critère de jugement CHECK pour le second critère (masse musculaire) CHECK pour le troisième (sarcopénie binaire)

Sur la sémiologie de la multiplicité des tests :

1. Écart au protocole, sur les analyses SUSPECT
2. Critères de jugements présentés dans la partie méthodes mais pas dans les résultats CHECK
3. Grande majorité (voire totalité) de petits p significatifs dans les résultats mais presque tous compris entre 0.01 et 0.05 CHECK
4. Étrangeté des analyses qui « tirent dans les coins » FAILED
5. Critère de jugement principal inattendu étant donné la population et l’intervention, voire disparition des critères de jugements attendus. FAILED

Conclusion

Avec un peu d’expérience, on peut identifier beaucoup de petits p bidons.