Vous avez peut-être entendu parler d’un résultat statistiquement significatif qui ne serait pas cliniquement significatif car correspondant à une différence trop faible, notamment à cause d’un échantillon « trop grand« . Le problème ne vient pas de la taille de l’échantillon mais du mauvais choix de l’hypothèse nulle. Si on veut prouver qu’un effet est cliniquement significatif, il faut que l’hypothèse alternative soit « cet effet dépasse le seuil de significativité clinique » et que l’hypothèse nulle en soit la négation, c’est-à-dire « cet effet est inférieur ou égal au seuil de significativité clinique ».
H0 : µ1-µ2 <= +clinthreshold
H1 : µ1-µ2 > +clinthreshold
Où clinthreshold représente le seuil de significativité clinique. On est habitué à ça pour les essais de non-infériorité, avec des seuils négatifs. Une analyse de supériorité devrait se faire de la même manière mais avec un seuil positif.
Évidemment, il ne faut pas se faire avoir par le syllogisme consistant à poser
H0 : µ1<=µ2
H1 : µ1 > µ2
puis rejeter H0 et conclure que la différence m1-m2 observée est la différence réelle et que, comme elle est supérieure au seuil de significativité clinique, on a prouvé qu’il existait un effet cliniquement significatif. En effet, dans le pire des cas, l’effet observé est égal au seuil de significativité clinique et l’affirmation selon laquelle l’effet réel est supérieur à ce seuil a un risque alpha unilatéral à 50%.
Pourquoi n’est-il pas pragmatique d’utiliser un seuil de significativité clinique ?
C’est trop subjectif. Comme tout ce qui est subjectif, les auteurs seraient tentés de tricher au maximum dessus (comme pour le delta du nombre de sujets nécessaires) et les reviewers pourraient toujours pinailler même si l’effet choisi par les auteurs est pertinent. Bref, ça pose des problèmes à tout le monde. Le zéro, par contre est objectif et consensuel même s’il est un des choix les moins pertinents qui soient.
Il y a d’autres problèmes, comme l’augmentation du nombre de sujets nécessaires (NSN), obligeant à tricher encore plus sur le calcul. La mascarade du NSN deviendrait encore plus évidente ; ce NSN est généralement calculé à l’envers, c’est-à-dire partant du nombre de sujets incluables pour en déduire les hypothèses nécessaires à générer ce nombre. Peut-être finirait-on par admettre qu’une étude ne répond pas de manière certaine à une question. Peut-être admettrait-on qu’il faut attendre la méta-analyse pour juger d’un effet et qu’un travail qui tente de répliquer un résultat a au moins autant de valeur sinon plus que l’article original, mais là, je rêve. Soyons réaliste, ça passerait mal.
Solution pragmatique : fournir un intervalle de confiance à 95% de l’effet et laisser le lecteur final de l’article déterminer lui-même si la borne basse dépasse ou non son seuil subjectif de significativité.
Poussons la réflexion
Vous l’aurez compris, ma formulation des hypothèses n’a qu’un intérêt conceptuel. Cela peut aider dans l’interprétation subjective de résultats et plus ou moins dans la construction méthodologique de projets de recherche, mais ne sera pas explicitement formulé.
Dans un essai clinique randomisé, on a généralement une hypothèse précise. On veut prouver la supériorité d’une intervention par rapport à une autre. Une vision « binaire » succès/échec est pertinente car la décision finale est binaire. En épidémiologie, on est parfois un peu plus neutre sur le sujet. Un cadre théorique à trois hypothèses paraît alors utilisable.
H0 : effet futile, c’est-à-dire -clinthresthold < effet < +clinthreshold
H1 : effet > clinthreshold
H2 : effet < clinthreshold
Si l’effet correspond à une différence entre deux groupes, alors on pourra reformuler :
H0 : équivalence
H1 : supériorité
H2 : infériorité
En analysant un intervalle de confiance, on pourra rejeter une ou plusieurs des trois hypothèses et fournir une conclusion plus ou moins fine.
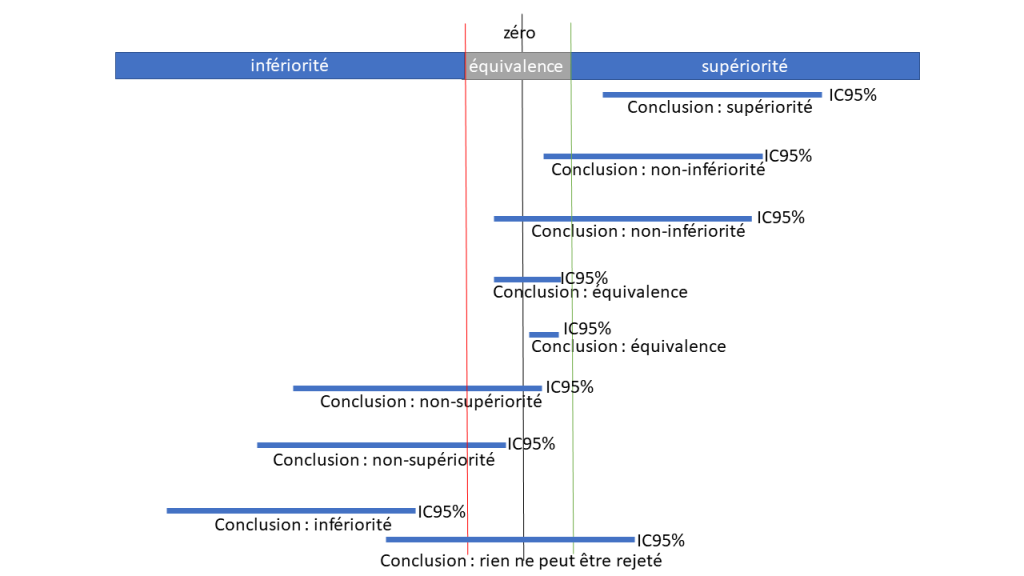
PS : un intervalle de confiance avec un niveau de confiance différent est possible, bien sûr.
Six conclusions différentes sont possibles dont trois sont tranchées, deux sont un peu floues et une est très floue :
Conclusions tranchées:
Supériorité : on a rejeté H0 et H2 et on accepte H1
Équivalence : on a rejeté H1 et H2 et on accepte H0
Infériorité : on a rejeté H0 et H1 et on accepte H2
Conclusions un peu floues:
Non-infériorité : on a rejeté H2 mais H1 comme H0 restent compatibles avec les données
Non-supériorité : on a rejeté H1 mais H2 comme H0 restent compatibles avec les données
Conclusion très floue: on n’a rejeté aucune hypothèse. Toutes les hypothèses restent compatibles avec les données.
Dans ce cadre conceptuel, on pourrait conclure à un différence significativement futile si la conclusion est l’équivalence… quand bien même le zéro n’est pas contenu dans l’intervalle de confiance de la différence.
De mon point de vue, ce n’est pas forcément aux auteurs de l’article de déterminer les seuils de significativité clinique, mais plutôt au lecteur de l’article. Par ailleurs, on pourrait pousser le concept plus loin en distinguant les effets cliniquement significatifs mineurs des effets cliniquement significatifs majeurs, les deux n’impliquant pas forcément la même réaction. En bref, la meilleure manière de « lire » un intervalle de confiance, c’est de tenter de conclure séparément sur l’effet observé à chacune des deux bornes de l’intervalle de confiance et de se dire que la réalité est probablement quelque part entre les deux (en négligeant les problèmes de prior bayésien ; ce qui est acceptable quand l’étude est de suffisamment grande taille pour que l’information du prior soit négligeable face à l’information contenue dans les données de l’étude).
Délire unilatéraliste
Vous avez pu déjà voir la formulation unilatérale suivante
H0 : µ1 = µ2
H1 : µ1 > µ2
Cette formulation est incorrecte à moins qu’il y ait une preuve mathématique que la proposition µ1 < µ2 soit fausse de telle sorte que µ1=µ2 est mathématiquement équivalent à µ1<=µ2. C’est le cas pour le test de Fisher dans une ANOVA, mais c’est loin d’être une situation habituelle.
En effet, rejeter l’égalité ne prouve pas la supériorité. Si on construit une statistique égale à la valeur absolue de la différence entre m1 et m2, on peut arriver à la conclusion que µ1 n’est pas égal à µ2 et rejeter H0, mais ça ne prouvera nullement la supériorité !
Une formulation plus correcte serait :
H0 : µ1 <= µ2
H1 : µ1 > µ2
On peut s’apercevoir que la P-value n’est pas aisément calculable dans ce cas, parce que si µ1 est légèrement inférieur à µ2 ou très largement inférieur, alors la distribution de M1-M2 change beaucoup. Eh bien, dans ce contexte, on prendra la borne supérieure des P-values spécifiques d’une différence donnée µ1-µ2 négative ou nulle. Si la statistique est bien conçue, il est probable que le pire des cas (P-value la plus grande) est dans le scenario µ1=µ2. C’est peut-être pour ça que certains ont mal formulé les hypothèses. Néanmoins la bonne formulation des hypothèses évite la construction de statistiques buggées qui ne se comportent pas bien dans le cas où µ1<µ2.
Délire bilatéraliste
Vous avez certainement vu la formulation
H0 : effet = 0
H1 : effet ≠ 0
Cette fois-ci H1 est bien la négation de H0, mais deux problèmes apparaissent.
- L’hypothèse nulle est souvent invraisemblable. Par exemple, paraît-il possible que le traitement chirurgical et le traitement médical de la hernie discale aient exactement le même résultat fonctionnel moyen à 12 mois ? La différence peut-être minime, complètement négligeable, mais la nullité absolue de la différence paraît impossible.
- L’hypothèse alternative est pratiquement inutile car elle ne donne ni d’information sur l’amplitude, ni sur la direction de l’effet. Dire qu’une exposition a un effet n’a pas spécialement de pertinence si on ne précise pas si elle est bénéfique ou nocive…
Si les analyses statistiques sont simples, alors on peut s’aider de l’effet observé pour juger de la direction de l’effet. Ce n’est pas le cas avec certains modèles de survie. Un bon exemple est le test MaxCombo décrit par Theodore Karrison dans l’article intitulé « Versatile tests for comparing survival curves based on weighted log-rank statistics » publié dans « The Stata Journal » (2016, Vol 16, Number 3, pp. 678-690). Le test permet de rejeter l’hypothèse de superposition parfaite de deux courbes de survie (hypothèse nulle) mais n’aide pas à décider de laquelle est la meilleure. Si on conclut, par exemple, que le groupe pour lequel la plus grande médiane de survie est observée, a réellement une médiane de survie supérieure, on prend un risque alpha unilatéral pouvant atteindre 50% dans le pire des cas. De même pour la survie à 1 an, pour l’espérance de vie tronquée, pour l’espérance de vie globale et à peu près pour tout ce qu’on peut imaginer.
Conclusion
Hypothèse nulle ne devrait pas être synonyme d’absence totale d’effet mais devrait toujours être la négation de l’hypothèse alternative, cette dernière étant l’hypothèse que l’on souhaite prouver. Commencez toujours par formuler cette hypothèse alternative et vous produirez des hypothèses nulles pertinentes. On peut créer des cadres théoriques distinguant plus d’hypothèses, mais la dualité H0/H1 reste pertinente pour les essais cliniques.