L’usage de tests de normalité n’est pas pertinente dans la recherche biomédicale. J’ai un point de vue très tranché sur la question car cet usage me paraît être une aberration à plusieurs sens, que je détaillerai ci-dessous.
1er argument : les lois du vivant ne sont pas normales
Pour rappel, la loi normale est une loi de distribution de variables quantitatives continues, pouvant prendre toute valeur réelle imaginable de moins l’infini (exclu) à plus l’infini (exclu).
Par principe, toute variable toujours positive ne peut pas suivre une loi normale. Une distribution discrète ne peut pas être normale, ni une distribution bornée. Voilà, j’ai déjà fait le tour de presque toutes les variables quantitatives que j’ai pu voir en recherche biomédicale, allant de l’âge aux concentrations moléculaires (toujours positifs), en passant par l’échelle visuelle analogique (EVA) de douleur, les échelles de qualité de vie (discrètes et bornées).
La normalité suppose aussi :
- Que la loi est parfaitement symétrique
- Que le kurtosis de la loi est exactement égal à 3
- Que tous les mouvements d’ordre supérieur sont parfaitement égaux à ceux d’une loi normale
- Qu’après centrage et réduction, la loi de distribution soit parfaitement superposable à celui d’une loi normale centrée-réduite
Si vous avez un doute, vous pouvez toujours consulter cet algorithme.
2ème argument : accepter l’hypothèse nulle est invalide
Pour faire bref, un test de normalité est aussi pertinent qu’un test d’immortalité construit ainsi
Hypothèse nulle H0 : le patient est immortel
Hypothèse nulle H1 : le patient est mortel
Procédure : attendre 1 an. Si le patient est décédé dans l’intervalle, rejeter l’hypothèse nulle H0, sinon, accepter le fait que le patient est immortel.
Cela est aberrant sur deux points : d’abord, cela nie le principe du raisonnement par l’absurde fondant les tests d’hypothèse. Il est pertinent de rejeter l’hypothèse nulle en cas de résultat significatif, mais il est erroné de rejeter l’hypothèse alternative (patient mortel) s’il n’est pas décédé sur une année. Un résultat non significatif, ne permet ni de rejeter, ni d’accepter l’une ou l’autre des hypothèses nulle et alternative. Il ne permet rien de conclure. Ensuite, c’est aberrant parce qu’on sait, dès le départ que tous les patients sont mortels (probabilité a priori = 100%). Le raisonnement réalisé lors de l’acceptation de l’hypothèse nulle est pourtant : jusqu’à preuve du contraire (test significatif), tout patient est immortel. Eh bien, j’inverse la charge de la preuve. Si on veut prouver qu’un patient est réellement immortel, il faut arriver à monter un protocole expérimental rejetant l’hypothèse selon laquelle il est mortel.
Il existe encore pire : la réalisation d’un test de normalité sur une variable ne pouvant, par principe, être normale, telle qu’une variable strictement positive (p.e. hémoglobine) ou discrète (p.e. échelle numérique de douleur de 0 à 10). Cela est équivalent à faire l’autopsie d’un patient dans l’espoir d’échouer à prouver qu’il est mortel pour pouvoir ensuite accepter le fait qu’il est immortel.
3ème argument : le test ne reflète pas le biais des analyses paramétriques
Les test de normalité sont souvent utilisés pour guider l’usage de tests paramétriques (p.e. test de Student) ou non-paramétriques (test de Mann-Whitney). Cela est basé sur l’idée que le test de Student repose sur une hypothèse de normalité. Même si ce test a été développé sur cette théorie, il est asymptotiquement non biaisé si les observations sont indépendantes et identiquement distribuées. Ainsi, il suffit que l’approximation normale de la différence de moyennes soit bonne pour que le test de Student soit valide.
Mon propos est le suivant : les tests de normalité mesurent très mal la qualité de l’approximation normale de la différence de moyennes.
En considérant la distribution comme fixe, plus l’échantillon est grand, plus l’approximation normale du Student est bonne, mais plus le test de normalité est puissant et donc tendra à « rejeter » l’usage du test de Student. Donc, pour une distribution donnée, en faisant varier N, on s’aperçoit que le test de normalité oriente vers la décision opposée à la décision pertinente.
Ensuite, pour un N fixé, les biais associés à l’inférence statistique, telle que l’inflation du risque alpha, sont dépendants de la distribution, mais d’une manière qui est mal décrite par le test de normalité.
Considérons, par exemple, le cas d’un test de Student sur séries appariées de supériorité (risque alpha unilatéral à 2.5%) sur un échantillon de taille 6. Si la distribution des différences appariées suit une loi exponentielle (à un décalage près pour que l’espérance soit zéro), alors le test de Shapiro a une puissance de 22% mais le risque alpha unilatéral du Student monte à 11%, soit une multiplication par un facteur supérieur à 4.4. Si la distribution suit une loi Beta(0.1, 0.1) alors la puissance du test est de 77% bien que le risque alpha unilatéral soit seulement multiplié par 1.03 (soit 2.57%, incertitude 2.566% à 2.579%). Si la distribution suit une loi binomiale de paramètres n=2 et p=0.50, alors la puissance du test est de 44% alors que le risque alpha unilatéral est réduit de 28% relatif (2.5% -> 1.79%). Si la distribution suit une loi de Student à 3 degrés de liberté, alors la puissance du test de normalité est de 11% pour un risque alpha unilatéral du Student descendant à 1.88% (incertitude 1.86 à 1.90%) soit une réduction de 25% relatif. Pour information, les distributions sont présentées ci-dessous :
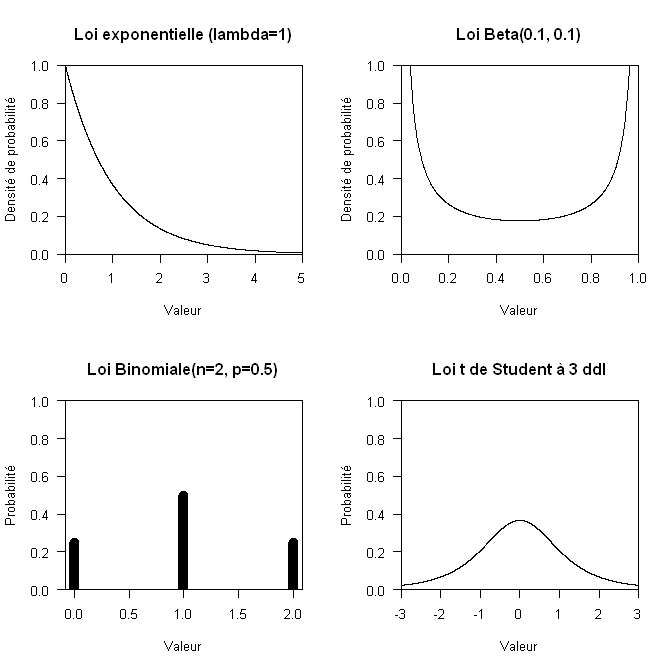
En bref, sur ces quatre exemples, la plus grande puissance du test de Shapiro porte sur la situation où le test de Student est le moins biaisé.
Le test de Shapiro est sensible aux kurtosis très bas (comme la loi beta) et aux distributions discrètes (comme la loi binomiale) alors que le test de Student résiste très bien à ces deux aspects. Le test de Shapiro est modérément sensible à l’asymétrie de la distribution, mais c’est cette dernière qui biaise le plus le test de Student.
Ensuite, les éléments suivants sont à prendre en compte dans l’évaluation des biais d’un test de Student :
- En présence de groupes de taille équilibrée (p.e. 15 vs 15), les asymétries des deux moyennes tendent à se compenser et le test de Student sur séries indépendantes est nettement moins biaisé qu’avec des groupes de taille déséquilibrés (p.e. 15 vs 150).
- Les conditions de validité d’un test de Student sur séries appariées reposent sur la distribution des différences appariées et pas la distribution de la variable aléatoire prise isolément dans chaque série de mesures ou dans les deux séries poolées. Par exemple, alors que le poids dans une population obèse, a une distribution asymétrique à droite, les différences de poids après moins avant traitement de l’obésité, suivent une loi plutôt asymétrique à gauche, de forme très différente de la première.
Il faut noter que chaque statistique a ses forces et fragilités. La régression passing Bablok (régression non paramétrique), par exemple, va avoir des problèmes de stabilité en cas de distribution discrète, là où la régression linéaire des moindres carrés y résistera très bien mais aura plus de difficultés à rester stable en présence d’outliers. À ce propos, en présence d’une distribution discrète, le test de normalité risquerait d’orienter vers le passing Bablok, car ce dernier est non paramétrique et donc « résistant aux écart à la normalité ».
4ème argument : les statistiques orientées par les statistiques sont ininterprétables
Faire un test de normalité pour orienter des choix statistiques ultérieurs, c’est méconnaître un des principes fondamentaux de la statistique fréquentiste : une même expérience doit conduire à une même statistique. Par ailleurs, il ne faut pas oublier qu’une statistique répond à une question. Une différence de moyennes peut s’estimer par la méthode de Student ou par du bootstrap paramétrique ou non paramétrique. Ce sont des estimateurs valides et asymptotiquement non biaisés (sauf sur la condition d’homoscédasticité de Student). Le test de Mann-Whitney n’est pas un test de comparaison de moyennes et son risque d’erreur de troisième espèce peut atteindre 100% s’il est interprété comme tel. À côté de cela, l’inflation du risque de première espèce, de 2.5% à 11% unilatéral, d’un Student sur une loi exponentielle avec n=6 est futile.
Pour poursuivre sur le risque d’erreur de troisième espèce sans changer de ton : http://www.numdam.org/article/RSA_1958__6_1_7_0.pdf