Un billet que j’écris suite à une remarque d’un reviewer qui a remis en cause ma manière de faire des analyses en sous-groupes, proposant une autre méthode, plus classique mais dont la validité est très discutable. Mes réflexions rejoignent une citation du Pr Bruno FALISSARD que je paraphrase ici, parce que je ne l’ai pas mémorisée de manière exacte : tout le problème est de savoir à qui est la charge de la preuve ?
Ce billet de blog contient du code R. Il n’est pas nécessaire à la compréhension du propos, mais peut vous aider à reproduire les résultats discutés et à comprendre comment ils ont été calculés.
Problématique
Une fois qu’on a mis en évidence le bénéfice d’un traitement sur un grand échantillon de sujets plus ou moins homogènes, cette homogénéité dépendant en partie des critères d’inclusion, on peut raisonnablement craindre que ce bénéfice ne soit pas identique chez tous les individus. Par exemple, on pourrait craindre qu’un traitement bénéfique sur une forme sévère de la maladie, soit inutile voire délétère sur une forme légère, comme on peut l’imaginer pour la dexaméthasone dans le traitement de la COVID-19. On parle alors d’interaction statistique. On distingue les interactions quantitatives des intraction pour lesquelles le traitement a un effet d’amplitude variable selon le sous-groupe mais reste toujours de même signe, des interactions qualitatives pour lesquelles le traitement a des effets opposés selon le sous-groupe: il serait nocif pour certains individus et bénéfique pour d’autres. Ce sont ces dernières interactions qui sont les plus préoccupantes, parce qu’elles remettent en cause la prescription à des sous-groupes identifiables, alors que des interactions quantitatives modestes ne changent pas grand chose aux indications et contre-indications.
Approche N°1 : tests en sous-groupes
La première approche, intuitive, à cette problématique, c’est de répéter le test d’efficacité dans chacun des sous-groupes (p.e. patients âgés, puis patients jeunes). Dans les sous-groupes pour lesquels on arrive à prouver l’effet bénéfique du traitement (p<0.05, IC95% effet = +10% à +30%), on est rassuré et on peut conclure sans crainte à son bénéfice. Dans les sous-groupes pour lesquels on échoue à prouver l’effet bénéfique ou nocif du traitement (p>0.05, IC95% effet=-20% à +30%), on admet qu’on ne peut pas conclure de manière certaine. Dans les sous-groupes pour lesquels on arrive à prouver un effet nocif (p<0.05, IC95% effet = -30% à -10%), on conclut qu’il est contre-indiqué.
Cette approche souffre d’une principale limitation. On manque souvent de puissance pour ces analyses en sous-groupes, conduisant à de nombreux tests non concluants (p>0.05). Si on avait une puissance à 90% avec risque alpha bilatéral à 5% (ou 2,5% unilatéral) pour l’analyse principale, incluant tous les sujets, et qu’on fait une analyse dans 3 sous-groupes parfaitement équilibrés (33% – 33% – 33% de l’échantillon complet), alors, sans même correction de multiplicité des tests la puissance descend à 46% dans chacun des deux sous-groupes, selon la formule R suivante:
pnorm((qnorm(0.975)+qnorm(0.90))/sqrt(3)-qnorm(0.975))Certains sous-groupes sont souvents plus petits qu’un tiers de l’échantillon complet, et la puissance de l’analyse principale est souvent inférieure à 90%, conduisant à beaucoup de résultats non concluants.
À ce problème, je répondrai que si on n’a pas les données, on ne va pas les inventer. Si on craint réellement à la nocivité d’un traitement dans un tout petit sous-groupe, mais qu’il est trop petit pour qu’on puisse retrouver l’effet dedans, alors on n’a vraiment pas la possibilité de se rassurer, sans lancer d’autres étude sur le sujet.
Variantes
Pour comprendre cette sous-section, il est préférable de lire les chapitres suivants. Revenez-y à la fin de votre lecture.
Doit-on faire une correction de multiplicité des tests ? Ça dépend un peu de l’intention. Si l’analyse principale démarre sur une recherche d’effets dans dix sous-groupes, avec une conclusion portant sur la ou les analyses qui ressortent statistiquement, alors le problème de multiplicité des tests s’applique et une correction paraît pertinente. Il n’est pas nécessaire de corriger la multiplicité des tests si l’analyse principale concerne l’effet global poolé, assumant la « dictature de la moyenne », puis que des analyses en sous-groupes sont faites pour faire joli, en analyse secondaire, mais que la conclusion ne dépend pas vraiment d’elles; on repose alors sur la présomption d’absence d’interaction (cf approche N°2) sécurisée par un choix pertinent de critères d’inclusion et d’exclusion (cf chapitre « les interactions qualitatives sont-elles fréquentes ? »). La non correction de multiplicité des tests est un moyen de remonter le risque alpha et d’améliorer la puissance, ce qui se rapproche du prior informatif (approche N°2). On pourrait aussi imaginer qu’on aille plus loin en remontant le seuil de significativité unilatéral de 2,5% à 5%, voire 10%. En pratique, le seuil de 5% bilatéral (2,5% unilatéral) est sacré; on ne peut pas y toucher; cependant on reste encore libre de tricher à mort avec la multiplicité des tests.
Approche N°2 : ajout d’une touche bayésienne
Cette approche N°2 n’est jamais employée même si elle pertinente; certainement en raison de l’obligation à intégrer une part de subjectivité. Cette seconde approche part du constat qu’avec de bons critères d’inclusion, les interactions qualitatives ou quantitatives fortes sont probablement rares. Pour illustrer cela, considérons le débat autour des vaccins anti-SARS-Cov-2 qui ont été tous principalement évalués chez des personnes jeunes (<= 65 ans) mais prescrits en premier chez des personnes âgés (>= 70 ans). D’abord, balayons une idée reçue ridicule. On ne peut pas conclure à l’efficacité d’un vaccin sur les personnes âgées en argumentant que 20% des patients étaient âgés et donc, qu’ils participent à l’analyse d’efficacité. En effet, si le vaccin était totalement inefficace chez les personnes âgées, alors les 80% de personnes jeunes pourraient très bien compenser cet effet nul du vaccin dans la statistique globale. Il est donc nécessaire de faire des analyses en sous-groupes, ou pas… De mon point de vue, subjectif, un vaccin efficace à plus de 90% chez des personnes d’âge moyen de 50 ans, pourrait être potentiellement un peu moins efficace sur des personnes âgés, mais une inefficacité totale chez la personne âgée paraît peu crédible; pas impossible, mais improbable. Je ne crois pas que ce phénomène d’inefficacité totale, passé un âge, ait jamais été rapporté pour un vaccin; les inefficacités majeures étant principalement rapportées chez des personnes fortement immunodéprimées. C’est ainsi, qu’avec une approche bayésienne, on aurait tendance à dire, qu’a priori, il y a de fortes chances que le vaccin ait une efficacité satisfaisante sur les personnes âgées, quand bien même l’échantillon n’en contient aucune ! L’expérience en population générale sur ces vaccins semble d’ailleurs avoir confirmé l’efficacité sur la personne âgée.
Une fois ce constat dressé, comment peut-on le traduire à termes statistiques ? Eh bien, on peut estimer les effets en sous-groupes avec une méthode bayésienne à prior informatif, considérant que la probabilité d’un effet proche de l’effet global est assez forte alors que la probabilité d’un effet nul ou négatif est faible, voire très faible. Le gros problème, c’est de régler la force de ce prior. Un prior d’informativité nulle, sera équivalent à l’approche N°1. En cas de résultat significatif, les conclusions seront très robustes, convainquant les bayésiens les plus sceptiques, mais bien souvent, les résultats ne seront pas concluants; ce qui n’est pas toujours un mal si on n’a réellement pas la donnée pour conclure. Au-delà une certaine force, le prior conduira à la conclusion d’un bénéfice en l’absence totale de donnée sur le sous-groupe; c’est-à-dire qu’on conclura au bénéfice du traitement avec N=0 observation. Ça peut paraître délirant, mais c’est loin de l’être; c’est ce qui a été fait par les autorités de santé publique qui ont recommandé les vaccins anti-SARS-Cov-2 aux personnes âgées alors que la quantité de données sur le sujet était négligeable ou nul. Un tel prior peut quand même conduire à remettre en cause l’efficacité du traitement si on dispose de suffisamment de données allant dans un sens contraire dans ce sous-groupe. En revenant au vaccin anti-SARS-Cov-2 et à la personne âgée : on part du principe que le vaccin est efficace chez la personne âgée, jusqu’à preuve du contraire; mais si on trouve une preuve du contraire, on est prêt à l’accepter. Même là, on peut régler le prior plus ou moins fortement, remettant en cause le bénéfice pour des preuves contraires faibles, ou au contraire exigeant des preuves contraires fortes.
Néanmoins je pense qu’il faut bien garder à l’esprit la distinction entre preuve et présomption. De mon point de vue, une conclusion à une efficacité basée sur N=0 est une présomption pas une preuve. Une présomption peut parfois être assez solide et des preuves peuvent être fragiles, mais la distinction pour moi, porte sur la source de données : la présomption est fondée sur un prior, et a une grand part de subjectivité alors que la preuve, même fragile, repose sur les données de l’étude (information contenue dans l’étude). Cette distinction est importante parce que la manière de remettre en cause la connaissance diffère. La preuve est remise en cause par la critique méthodologique de l’article alors que la présomption est remise en cause par la faible validité des connaissances externes ou surtout de leur articulation qui ont conduit à cette présomption.
C’est aussi sur cette présomption que tous les cliniciens reposent tous les jours en prescrivant des traitements à des patients pour lesquels il n’y a jamais eu d’analyse en sous-groupes ou pour lesquelles elles ne sont pas du tout concluantes ; c’est-à-dire la grande majorité des sous-groupes.
Comme cette approche N°2 n’est jamais appliquée formellement en pratique, que je ne l’ai moi-même jamais appliquée, je ne saurais pas vous conseiller sur la mise en oeuvre, et notamment le choix du prior.
Approche N°3 : échouer joyeusement au test d’interaction
Présentation
C’est cette approche N°3 que le reviewer m’a proposée. Elle viole allègrement les principes fréquentistes mais peut avoir une interprétation intéressante si on la regarde sous un autre angle. La procédure est la suivante:
Faire un test d’interaction, dont l’hypothèse nulle est : l’effet du traitement est identique dans tous les sous-groupes (p.e. identique chez les personnes âgées et les jeunes). Si on échoue à rejeter cette hypothèse nulle, alors l’accepter comme une vérité solide et conclure à l’équivalence des effets dans tous les sous-groupes. Cela permet alors de ne plus présenter les effets des sous-groupes mais juste un unique effet principal que l’on considère comme applicable à tous les sous-groupes. À l’opposé, si le test d’interaction est significatif, alors on considère que l’effet principal n’a plus de sens, et on présente seulement les effets des sous-groupes.
Problème conceptuel : acceptation de l’hypothèse nulle en situation de sous-puissance
Cette approche repose sur l’acceptation de l’hypothèse nulle dans une situation de puissance statistique catastrophique. On n’a pas les moyens de voir quoi que ce soit et on se rassure faussement en disant qu’on n’a rien vu. En fait, la puissance du test d’interaction est généralement très inférieure à celle des tests réalisés dans l’approche N°1.
Considérons par exemple une population dans laquelle il y a deux sous-groupes équilibrés (prévalences 50% / 50%), ce qui est un scenario très favorable. Une puissance à 90% aurait été calculée pour l’analyse principale, poolant les deux sous-groupes avec un effet +X. L’effet réel serait effectivement égal à +X dans le premier sous-groupe mais serait nul dans le second sous-groupe. L’approche N°1 conduirait à une puissance à 63% pour le premier sous-groupe:
pnorm((qnorm(0.975)+qnorm(0.90))/sqrt(2)-qnorm(0.975))Avec l’approche N°1, le risque alpha serait à 5% pour le second sous-groupe et la notion de puissance ne s’appliquerait pas, puisque l’effet du sous-groupe est nul.
Avec l’approche N°3, la puissance du test d’interaction serait de 37%:
pnorm((qnorm(0.975)+qnorm(0.90))/sqrt(2*2)-qnorm(0.975))En effet, ce test d’interaction est basé sur la différence d’effet entre deux groupes indépendants, avec les variances des effets qui se cumule; pour deux groupes de même taille avec des effets estimés de même précision, cela double la variance. La puissance diminue encore beaucoup si l’interaction est quantitative, avec, par exemple, un effet deux fois plus petit pour le second groupe que pour le premier. En effet, l’interaction à estimer vaudra alors X/2 plutôt que X, conduisant à une puissance à 12,5%:
pnorm((qnorm(0.975)+qnorm(0.90))/sqrt(2*2*4)-qnorm(0.975))Et cela est pourtant estimé dans un scenario favorable, avec des groupes bien équilibrés, peu nombreux (2 sous-groupes seulement), et une puissance initialement calculée à 90%. Face à une puissance aussi ridicule, un test significatif perd en pertinence, puisque cette significativité est presque aussi probable sous l’hypothèse nulle que sous l’alternative; il n’est alors plus discriminant entre les deux et un résultat significatif ne fournit presque plus d’information sur la valeur de véracité de l’une ou l’autre des hypothèses. Il faut donc ignorer complètement les résultats d’un test significatif comme d’un test non significatif.
Interprétation abusive et comparatisme
Certes, l’interaction quantitative est beaucoup moins préoccupante que l’interaction qualitative, mais un test d’interaction échoué va donner l’illusion d’une preuve d’homogénéité des effets, comme le reviewer mentionnait, conduisant à généraliser l’intervalle de confiance de l’analyse poolée à tous les sous-groupes. Il me paraît plus honnête de se limiter à prouver qu’il existe un effet bénéfique dans chaque sous-groupe, sans les comparer les uns aux autres, ce qui est déjà très difficile à faire (approche N°1).
Ensuite, les tests d’interactions quantitatives ont d’autres problèmes. Sur de très grands échantillons, ce qui n’est pas courant mais arrive parfois, ils peuvent avoir une très bonne puissance et conclure à la non homogénéité de l’effet des traitements; rien de mal à ça, sauf que ça risque de conduire à la pratique du comparatisme; tendance à conclure, à tort, qu’un sous-groupe ne bénéficie pas du traitement seulement parce que son bénéfice est inférieur à celui d’un autre groupe. De mon point de vue, en situation de grand échantillon (aucune incertitude), l’évaluation de la balance bénéfices/risques dans un sous-groupe ne doit pas dépendre des autres sous-groupes. Si on considère qu’un bénéfice de +30% est bon, alors le sous-groupe A qui aura un effet de +31% aura une indication au traitement, peu importe que le groupe B ait un effet de +80%, de +31% ou de +15%. C’est l’approche N°1 qui permet de raisonner de cette manière alors que l’approche N°3 encourage très fortement à ne s’intéresser qu’à la comparaison des effets les uns aux autres.
Validité statistique conditionnelle
Dans cette approche, on n’évalue séparément les effets des différents groupes, seulement si le test d’interaction est significatif. En raison de la faible puissance qui y est généralement associée, le test ne sera significatif que si l’hétérogénéité observée est très largement supérieure à la l’hétérogénéité réelle (dans la population). L’interaction aura l’air énorme alors qu’il s’agira en réalité d’une interaction finalement modeste, voire nulle. Dans les cas où il existe une interaction réelle et modeste, mais la puissance est très faible (< 10%), il y aura de forts risques que l’interaction significative observée soit de signe opposé à l’interaction réelle et qu’on conclue, à tort que le sous-groupe de moindre bénéfice et celui de plus fort bénéfice !
Considérons une étude qui a été conçue avec une puissance à 80% pour mettre en évidence un effet +X. Cet effet s’avère être de +X dans le sous-groupe principal A représentant 75% de l’échantillon mais n’est que de 0.80×X dans un sous-groupe complémentaire B représentant 25% de l’échantillon. La probabilité d’observer une interaction significative du même signe que l’interaction réelle est de 4,3%:
pnorm((qnorm(0.975)+qnorm(0.80))/sqrt(1/0.25 + 1/0.75)*(1-0.80)-qnorm(0.975))alors que la probabilité d’observer une interaction significative de signe opposé à l’interaction réelle est de 1,4%:
1-pnorm((qnorm(0.975)+qnorm(0.80))/sqrt(1/0.25 + 1/0.75)*(1-0.80)+qnorm(0.975))Conditionnellement au fait que l’interaction soit significative, on a quand même 24% de risque de conclure à l’existence d’une interaction dans le sens opposé au sens réel de l’interaction !
Conditionnellement à un résultat significatif de signe correct (c’est-à-dire dans les 4,3% de bons scenarii), on estimera en moyenne l’effet du groupe A à 1.44×X (alors que c’est en réalité 1×X) et l’effet du groupe B à −0.51×X (alors que c’est en réalité 0.80×X) et on estimera la différence à 1.95×X en moyenne alors qu’elle est en réalité c’est 0.20×X. On conclura donc à une interaction majeure et on doutera très fortement du bénéfice dans le groupe B alors qu’en réalité il est presque équivalent à celui du groupe A. Il est même possible que certains concluent à tort à l’existence d’une interaction qualitative.
Conditionnellement à un résultat significatif de signe incorrect (dans 1,4% de cas), on estimera en moyenne l’effet du groupe A à 0.47×X (alors qu’en réalité c’est 1×X) et l’effet du groupe B à 2,38×X (alors qu’en réalité c’est 0.80×X), ce qui conduira à des estimations fortement erronnées mais heureusement ne conduira pas à la conclusion de l’existence d’une interaction qualitative en général.
L’histogramme ci-dessous est très parlant, car il montre que la directive du reviewer consistant à ne regarder l’interaction qu’en cas de significativité conduit à une estimation de ce terme d’interaction qui est tout sauf pertinente:
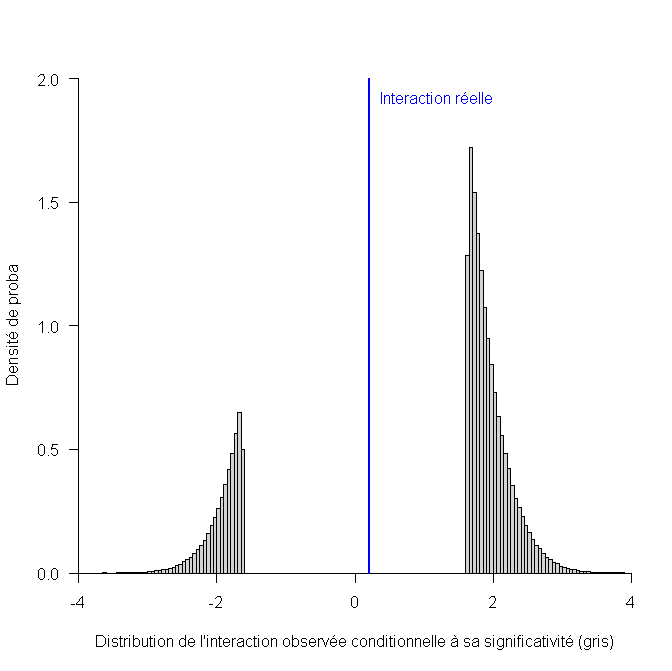
Alors que l’interaction réelle est de 0.20, l’interaction estimée sera toujours très grande ou très petite : à coup sûr inférieure à -1.62 ou supérieure à +1.62, mais jamais entre les deux.
Le code R qui permet de réaliser ces simulations est:
# simulations distributions des effets
# dans chacun des deux groupes
r1=rnorm(1e7, mean=1.00, sd=sqrt(1/0.75)/(qnorm(0.975)+qnorm(0.80)))
r2=rnorm(1e7, mean=0.80, sd=sqrt(1/0.25)/(qnorm(0.975)+qnorm(0.80)))
# standard error du terme d'interaction
SE=sqrt(1/0.75 + 1/0.25)/(qnorm(0.975)+qnorm(0.80))
ok=abs(r1-r2)/SE > qnorm(0.975) # significatif
# significatif dans le bon sens
round(mean(r1[ok & (r1-r2)>0]),2)
round(mean(r2[ok & (r1-r2)>0]),2)
# significatif dans le mauvais sens
round(mean(r1[ok & (r1-r2)<0]),2)
round(mean(r2[ok & (r1-r2)<0]),2)
# histogramme
hist(r1[ok]-r2[ok],breaks=200,prob=TRUE,
las=1,main="",xlim=c(-4,4),
xaxs="i",yaxs="i",ylim=c(0,2),
ylab="Densité de proba",
xlab="Distribution de l'interaction observée conditionnelle à sa significativité (gris)")
text(x=0.2,y=1.9,"Interaction réelle",adj=c(-0.1,0),col="blue")
abline(v=0.2,col="blue",xlab="Interaction observée",lwd=2)
J’ai aussi créé un code presque exact, basé sur la fonction de densité de proba de la loi normale, approchée par une loi discrète:
x=seq(-5, 5, 0.01)
g1=prop.table(dnorm(x, mean=1.00,
sd=sqrt(1/0.75)/(qnorm(0.975)+qnorm(0.80))))
g2=prop.table(dnorm(x, mean=0.80,
sd=sqrt(1/0.25)/(qnorm(0.975)+qnorm(0.80))))
SE=sqrt(1/0.75 + 1/0.25)/(qnorm(0.975)+qnorm(0.80))
df=cbind(expand.grid(x1=x,x2=x),
expand.grid(p1=g1,p2=g2))
df$delta=df$x1-df$x2
df$signif=abs(df$delta)/SE >= qnorm(0.975)
df$proba=df$p1*df$p2
xdf=subset(df, signif)
ok=xdf$delta>0
round(sum(prop.table(xdf$proba[ok]) * xdf$x1[ok]),2)
round(sum(prop.table(xdf$proba[ok]) * xdf$x2[ok]),2)
round(sum(prop.table(xdf$proba[ok]) * xdf$delta[ok]),2)
ok=xdf$delta<0
round(sum(prop.table(xdf$proba[ok]) * xdf$x1[ok]),2)
round(sum(prop.table(xdf$proba[ok]) * xdf$x2[ok]),2)
max(xdf$delta[xdf$delta<0])
min(xdf$delta[xdf$delta>0])Hypothèse nulle difficile à croire
L’hypothèse nulle d’homogénéité parfaite des effets est difficilement plausible pour les analyses en sous-groupes concernant les facteurs pronostics. En effet, selon que l’on utilise un modèle ou un autre, il y aura une interaction ou pas. Par exemple, si on considère un pourcentage de résultat favorable sous traitement à 30% dans le groupe A contre 20% sans traitement et un résultat favorable sous traitement à 40% dans le groupe B contre 30% sans traitement, les deux effets sont à +10% (modèle linéaire), mais les rapports de pourcentages, odds ratio ou effets dans un modèle probit, diffèrent. Ces modèles sont fondamentalement contradictoires sur leur conception de l’homogénéité des effets lorsque le niveau de base diffère selon le sous-groupe. Il n’y a aucune raison qu’un de ces modèles soit vrai car ils ont été simplement conçus pour des raisons de simplicité mathématique. En conséquence, l’absence totale d’interaction, dans l’un ou l’autre de ces modèles, paraît presque impossible. L’interaction peut être faible, mais elle ne devrait pas être nulle. C’est donc d’autant plus difficile d’accepter une hypothèse nulle d’homogénéité parfaite sachant que cette hypothèse est très peu plausible a priori.
Variante
Gail & Simon ont proposé un test d’interaction qualitative (Biometrics. 41 (2). 1985, pp. 361-372, doi:10.2307/2530862), qui évite la tendance au comparatisme et recentre le débat sur le problème des interactions vraiment préoccupantes. Malheureusement ce test aggrave énormément le problème de sous-puissance statistique et d’acceptation abusive de l’hypothèse nulle parce qu’il va globalement, ne fournir de résultat significatif que si un sous-groupe montre un effet significativement positif alors que l’autre montre un effet significativement négatif.
Synthèse des approches
L’approche bayésienne (approche N°2) est la plus générale et permet de bien comprendre les enjeux, même si elle est probablement difficile voire impossible à appliquer en pratique. L’approche N°1 est équivalente à une approche bayésienne (N°2) à prior non informatif. L’approche N°3 se rapproche de l’approche N°2 avec un prior absolument massif, complètement déraisonnable, et conduit à conclure abusivement à l’homogénéité de l’effet dans presque tous les cas; dans les rares cas où cette méthode arrive à montrer l’hétérogénéité de l’effet, les effets estimés sont extrêmement éloignés de la réalité, ce qui peut tromper encore plus que si on concluait à l’homogénéité. Dans la majorité des cas cette approche N°3 fait passer une présomption d’homogénéité pour une preuve, en renversant la charge de la preuve. Mais dans les rares cas où le test est significatif, la présomption (prior bayésien) s’efface brutalement conduisant à une conclusion complètement différente. C’est ainsi qu’une observation peut renverser brutalement (en passant de p=0.051 à p=0.049) les conclusions qui passent de « parfaite homogénéité » à « hétérogénéité absolument majeure », et cela, de manière très faiblement corrélée à l’existence d’une réelle hétérogénéité.
Notion d’effet moyen
Un problème avec l’approche N°3, c’est de ne pas assumer que même en présence d’interaction, l’effet poolé reste interprétable comme l’effet moyen du traitement donné à la population complète. Cet effet moyen est particulièrement pertinent lorsque le « traitement » est une exposition nocive ou bénéfique, difficile à contrôler individuellement, et qui, en conséquence est imposé à la population entière. À condition que l’échantillon soit représentatif, l’effet global représentera le bénéfice ou la nocivité collective. En cas de non représentativité de l’échantillon, on pourra éventuellement repondérer.
Pour bien interpréter un effet global comme un effet en sous-groupe, il est nécessaire de bien comprendre qu’en statistiques, on va toujours calculer des effets moyens, qui ne sont pas applicables à un niveau individuel. L’effet d’un traitement sera positif en moyenne s’il fait plus de bien que de mal, mais le bien et le mal ne concernent souvent pas les mêmes patients. Les effets indésirables sont très imprévisibles, de même que l’efficacité qui est très variable; c’est pour ça que même une étude en cross-over, effaçant les différences sur de très nombreuses variables observables comme inobservables entre les groupes, peut nécessiter de nombreux patients pour mettre en évidence une moyenne positive de l’effet. Philosophiquement, on doit pouvoir distinguer des effets « non déterministes ou apparentés » et les effets déterministes inconnus. Les effets « non déterministes ou apparentés » sont les effets que l’on peut considérer comme « totalement aléatoires », parce qu’ils ne seront jamais prévisibles, peu importe le nombre et la finesse des variables qu’on a mesurées. Après tout, le résultat d’un lancer de dé est totalement imprévisible, quand bien même la position et la vitesse initiale du dé sont parfaitement contrôlées et mesurées; même à un niveau subatomique, les mouvements d’un électron autour d’un noyau d’hydrogène sont totalement imprévisibles et doivent être modélisés par une fonction de densité de probabilité de présence (orbitale); le vivant est encore mois prévisible. Néanmoins, il existe aussi probablement des effets déterministes inconnus, sur des variables qui ne sont pas connues du tout ou pas mesurées habituellement (p.e. sous-type histologique de biologique moléculaire d’un cancer); il peut y avoir des interactions qualitatives sur ces variables, qui seront éventuellement connues à l’avenir. En l’absence de connaissance de ces variables d’interaction, on va évaluer l’effet du traitement sur un groupe comportant un mélange de patients avec un effet positif et de patients avec un effet négatif; selon le ratio des groupes et des effets, on pourra avoir un effet moyen positif. On considèrera alors qu’en moyenne, le traitement est bénéfique et on le donnera à tous les patients. Est-ce à tort ou à raison ? C’est une question philosophique à laquelle je répondrai qu’en l’absence de connaissance dur la variable inconnue, c’est à raison que l’on donne le traitement à tout le monde, car cela fournit la meilleure espérance au patient, compte-tenu des connaissances médicales actuelles; l’alternative est de ne pas donner le traitement, ce qui aura une espérance négative. La situation dans laquelle on a une puissance très insuffisante pour faire des analyses en sous-groupes n’est pas si différente; les connaissances actuelles ne permettent pas de répondre à la question du bénéfice dans chacun des sous-groupes, mais disent qu’en moyenne, il y a un bénéfice sur la population globale; on fait alors au mieux avec les connaissances actuelles. En réalité, ça dépend un peu de la force de la présomption d’interaction qualitative. Si cette présomption était forte, on s’obligerait à conclure sur les deux analyses en sous-groupes séparément (cf approche N°1). C’est pourquoi, par exemple, on ne mélange pas les enfants et les adultes dans l’évaluation des traitements psychiatriques, craignant fortement les interactions qualitatives.
Les interactions qualitatives sont-elles fréquentes ?
Les interactions qualitatives sont légion, mais on les voit rarement, parce qu’on les anticipe dans les critères d’inclusion et d’exclusion ! Depuis qu’on a abandonné la recherche de la panacée, on sait très bien que le traitement doit être adapté au malade parce qu’un traitement inadapté à de très forts risques de faire plus de mal que de bien. C’est pourquoi il est nécessaire de faire des diagnostics ! Selon l’étiologie d’une dyspnée, par exemple, le traitement sera très différent, et en administrant le mauvais traitement, on aura de forts risques d’aggraver l’état du patient. C’est pour ça qu’il faut dix ans d’étude pour avoir le droit de prescrire ces traitements : mal utilisés ils font plus de mal que de bien. Les projets de recherche prennent toujours en compte ces interactions en définissant, par des critères d’inclusion et de non-inclusion, une population suffisamment homogène pour que la présomption d’interaction soit faible. Dans les rares cas où la présomption d’interaction reste assez forte mais on espère néanmoins qu’il y aura un bénéfice dans deux sous-groupes, on peut planifier directement une analyse en sous-groupes selon l’approche N°1.
Quelques éléments supplémentaires sur le case report
Même si les exemples que j’ai pris sont calqués sur l’évaluation thérapeutique, la problématique est très semblable pour d’autres types d’étude, notamment les études diagnostiques. La question du reviewer portait justement sur une étude diagnostique dans laquelle on évalue l’apporte de l’intelligence artificielle au diagnostic radiologique de fractures. L’apport de l’intelligence artificielle, en sensibilité et spécificité, dépend potentiellement de la localisation de la fracture; le carpe ou les cotes ne sont pas le même problème, ni pour l’humain ni pour la machine. Contrairement à la plupart des études, celle-ci était très largement dimensionnée et conçue pour les analyses en sous-groupes. L’étude porte sur 480 examens radiographiques lus par 24 lecteurs. Tous les lecteurs lisaient tous les examens, avec et sans aide de l’intelligence artificielle avec une période de wash-out, ce qui conduisait à 24×480×2 = 23040 lectures. Comme la principale source de variance était le lecteur, les analyses en sous-groupes par localisation de l’examen radiographique portaient sur le même nombre de lecteurs (n=24) mais pas le même nombre d’examens (n < 480), ce qui baissait finalement modérément la puissance statistique par rapport à l’analyse principale. Au total, avec l’approche N°1, sur les 9 localisations considérées, on arrivait à montrer un apport positif de l’intelligence artificielle sur la sensibiltié pour 7 d’entre-elles et on échouait pour 2 d’entre elles au seuil de significativité 2,5% unilatéral (ou 5% bilatéral) sans correction de multiplicité des tests. En montant le niveau de significativité à 7,5% unilatéral (15% bilatéral), on montrait le bénéfice pour 8/9. Selon l’approche N°1, il est impossible de dire si pour les « 2 échecs », il n’y a pas de bénéfice de l’intelligence artificielle, s’il est plus faible que pour les autres localisations, ou si ce sont des échecs attribuables à de simples fluctutations d’échantillonnage défavorables. La présomption de forte interaction, voire d’une interaction qualitative, en raison de possibles effets pervers de l’aide, était loin d’être négligeable, mais on arrive quand même à avoir une conclusion assez forte sur 7 localisations et un doute pour les deux dernières.