Résumé
Ce billet discute de l’ajustement dans les essais cliniques en randomisation individuelle. Il montre que l’ajustement statistique fait peu gagner en puissance, permet parfois de rectifier un défaut de randomisation, mais pose aussi des soucis non négligeables :
- P-hacking plus ou moins important
- Erreurs de manipulation du logiciel
- Résultats théoriquement non biaisés mais ininterprétables (odds ratio conditionnel à une variable inobservée), en pratique interprétables mais biaisés (car interprétés comme odds ratio marginal ou conditionnel aux variables observées)
- Résultats mal présentés (p.e. odds ratio conditionnel plutôt que différence absolue de risques)
- Les hypothèses faites par les modèles (absences d’interactions, linéarité) sont fausses, et cela peut conduire à un biais dans les estimations
Une partie de ces problèmes disparaît ou s’atténue lorsqu’on utilise exclusivement le modèle linéaire gaussien, qu’on ajuste seulement sur la covariable pronostique majeure, qu’on s’assure que le protocole soit publié avec un paragraphe statistique très exhaustif.
Je conseille d’avoir conscience de ces problèmes afin d’utiliser avec parcimonie, et en toute connaissance de cause, les ajustements dans les essais cliniques en randomisation individuelle.
Introduction
Dans un essai clinique randomisé bien mené, il n’y a pas de facteur de confusion car l’allocation des traitements est aléatoire et donc indépendante de tout facteur pronostique ou pas. Un ajustement statistique sur des facteurs pronostiques est possible, avec ou sans stratification de la randomisation. Cet ajustement réduit les fluctuations d’échantillonnage explicables par les déséquilibres aléatoires entre les groupes sur ces facteurs pronostiques, ou, dans le cadre de la randomisation stratifiée, évite une surestimation des fluctuations d’échantillonnages, en excluant du calcul de la variance résiduelle, la variance ou plutôt la non-variance des facteurs pronostiques. Au final, cela augmente la puissance sans modifier le risque alpha. Comme dans l’évaluation de toute méthode statistique, deux questions doivent être posées : que gagne-t-on ? que perd-on ?
Que gagne-t-on ?
Le gain de puissance est maximal lorsque le facteur pronostique expliquant une grande partie de la variance de l’outcome. En pratique, cela veut dire que le facteur pronostic est fortement lié à l’outcome et a une grande variance. Pour un facteur pronostique binaire, l’idéal est une prévalence de 50% (forte variance) et que selon sa présence ou non, l’outcome soit très favorable ou défavorable.
Nous prendrons comme référence, un cas d’école dans lequel le facteur pronostique est majeur et a une forte variance : le stade selon l’American Joint Committee on Cancer (AJCC) du cancer du colon, communément appelé stade TNM. Nous prenons comme référence la version 6 (O’Connell J, Maggard M, Ko C. Colon Cancer Survival Rates With the New American Joint Committee on Cancer Sixth Edition Staging. Journal of National Cancer Institute, Vol. 96, No. 19, October 6, 2004) car elle est en accès libre et dispose de tables de mortalité et de prévalences précises contrairement aux versions 7 et 8. La figure ci-dessous montre la distribution jointe du stade et de la mortalité à 5 ans.
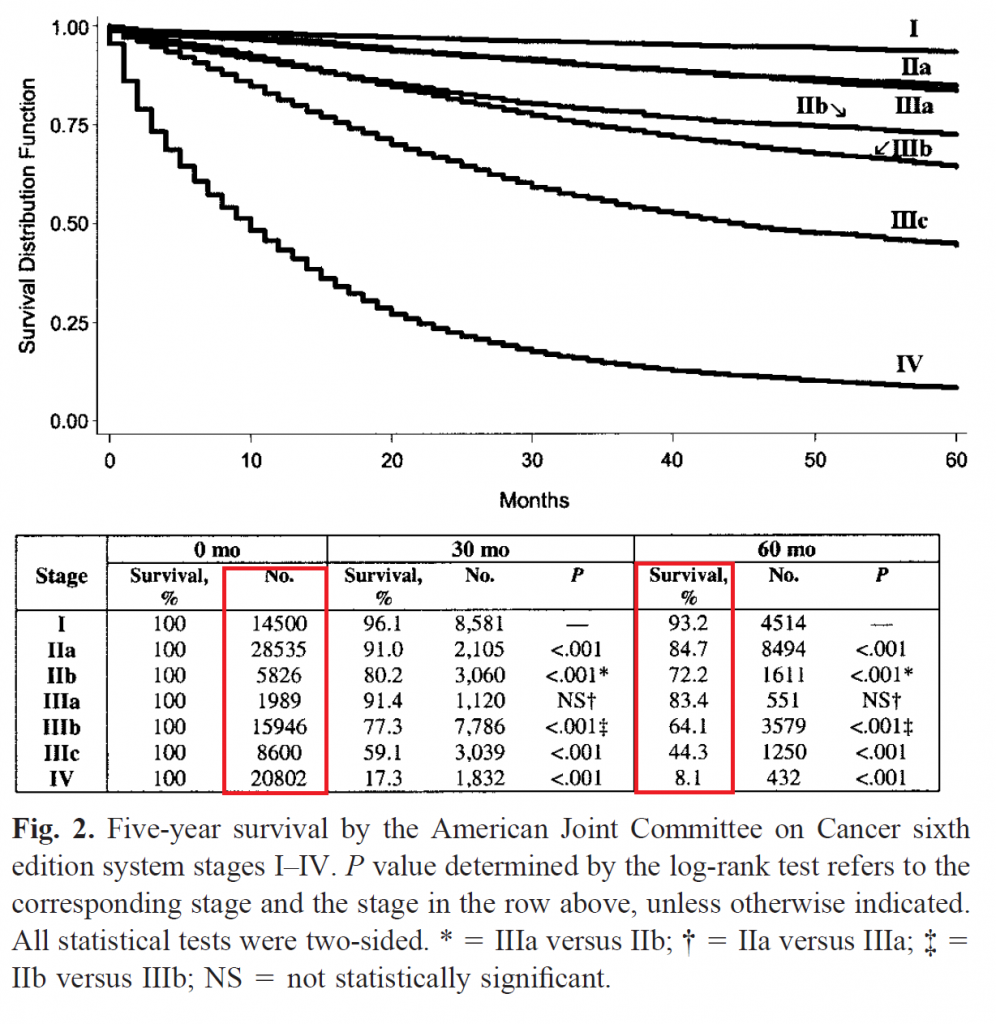
Un facteur pronostique capable de séparer 8.1% de mortalité de 93.2%, ainsi que de nombreux risques intermédiaires, avec une variance aussi grande n’est pas commun dans les essais cliniques. Il faut noter qu’un essai clinique n’inclura pas des stades I et des stades IV. Le pronostic et le traitement de référence dépendant beaucoup du stade, un essai clinique inclura un seul stade (exemples : https://dx.doi.org/10.1056/NEJMoa1713709, https://dx.doi.org/10.1001/jamaoncol.2019.6486). Autrement, mélanger des patients ayant des stades très différents ouvre la porte à des interactions et la sélection d’un traitement bénéfique à un sous-groupe (p.e. stade III) mais nocif à un autre (p.e. stade II), sans que la distinction ne soit faite entre les deux stades. En bref, un tel facteur pronostic majeur ne devrait pas exister à l’intérieur d’un essai clinique. Considérons dans un premier scenario qu’il soit possible d’inclure des stades I (tumeur localisée ne dépassant pas la muqueuse) et des stades IV (tumeur avec métastases à distance) dans un même essai clinique.
Nous ne nous intéresserons pas aux modèles de survie basés sur les risques proportionnels, qui ont leur propres problèmes, mais plutôt considèrerons la mortalité binaire à 5 ans.
Le 1er scenario est basé sur une puissance à 80%, un risque alpha unilatéral à 2.5% (ou bilatéral à 5%) dans un modèle ajusté sur le stade tumoral (7 modalités -> 6 variables binaires recodées) en randomisation simple 1:1 dans un modèle linéaire gaussien pour une intervention correspondant à un odds ratio conditionnel à 0.50 (facteur protecteur) sur la mortalité à 5 ans. L’omission d’un ajustement est à l’origine d’une inflation de l’erreur type (standard error) par un facteur 1.32, correspondant à une réduction de la puissance de 80% à 56.4%. Pour atteindre la même puissance à 80%, il faut multiplier par 1.75 le nombre de sujets, passant de 519 sujets à 907 sujets. Le gain en terme de puissance est peu dépendant de l’effet du traitement. Un odds ratio à 0.25 conduit à une perte de puissance de 80% à 57.1% lors du non-ajustement alors qu’un odds ratio à 0.95 conduit à une perte de puissance de 80% à 57.4% lors du non-ajustement. Cela est dû au fait que la perte de puissance dépend seulement de la variance expliquée par le facteur pronostique, qui dépend de la prévalence et de la moyenne des outcomes les deux groupes étant poolés. Cette moyenne des outcomes dépend un peu de l’effet du traitement.
Le 1er scenario montre un intérêt important de l’ajustement mais n’est pas réaliste du tout. Aucun essai clinique n’inclurait des stades I à IV. Le 2ème scenario, encore loin de la réalité, est basé sur l’inclusion des stades I à III (tumeur très localisée, jusqu’à tumeur avec envahissement local important touchant les organes voisins et métastases ganglionnaires régionales nombreuses). Dans ce cas là, le non-ajustement (avec odds ratio à 0.50) conduit à une inflation de l’erreur type par 1.061, une réduction de la puissance de 80% à 75.2% ou une augmentation du nombre de sujets nécessaires de 12.5%. Comme dans le 1er scenario, l’effet du traitement n’a pas vraiment d’importance.
Le 3ème scenario est identique au second même une régression logistique est employée plutôt qu’une régression linéaire. La perte de puissance est presque la même que dans le modèle linéaire, à une différence absolue de puissance de 0.98% près. Par contre, le modèle logistique risque d’être mal interprété. En effet, le bénéfice de traiter tous les sujets avec le traitement innovant correspond à une réduction de la mortalité à 5 ans de 38.4% à 29.6% correspondant à une différence absolue de risque de 8.8% (meilleur manière d’en quantifier le bénéfice) ou à un odds ratio marginal de 0.675. L’odds ratio conditionnel au stade, par contre, est égal à 0.50 (soit 0.74 fois l’odds ratio marginal). C’est cet odds ratio conditionnel que les logiciels statistiques fournissent en sortie. Plus l’ajustement porte sur un facteur pronostique pertinent, plus l’odds ratio conditionnel s’écarte de l’odds ratio marginal. En l’absence d’ajustement, la régression logistique fournit l’odds ratio marginal, plus simple à interpréter car indépendant du nombre et de la nature des variables d’ajustement.
Le 4ème scenario, plus réaliste, consiste en l’ajustement sur le stade a, b ou c chez des patients tous en stade III, en conservant les autres paramètres (odds ratio conditionnel à 0.50, puissance à 80%, risque alpha à 2.5% unilatéral), dans un modèle linéaire gaussien. L’inflation de la variance due au non-ajustement est de 1.025 avec une perte de puissance de 1.97% (80% -> 78.03) ou un nombre de sujets nécessaires augmenté de 5.1%.
En bref, l’ajustement sur un facteur pronostique important et de forte variance, dans des conditions réalistes, peut faire gagner 2% de puissance soit 5% de sujets à recruter en moins. Il paraît déjà impossible de gagner 5% de puissance car il faudrait une hétérogénéité majeure de la population (stades I à III mélangés), ce qui conduirait à une réduction du nombre de sujets nécessaires d’environ 11%. On peut donc conclure que le gain, en nombre de sujets nécessaires sera toujours inférieur à 10%, et sera souvent situé en dessous de 5%. La présence de multiples facteurs pronostiques fournit rarement une capacité pronostique supérieure à celle du stade dans les cancers du colon. Par exemple, le Karnofsky n’est pas pris en compte dans le stade AJCC, probablement parce qu’il n’influence pas de manière majeure le pronostic.
Un second bénéfice, non négligeable de l’ajustement, c’est l’adaptation aux situations où l’essai clinique randomisé n’a pas été bien mené telle qu’une mauvaise randomisation ce qui peut arriver, par exemple, dans un essai en ouvert avec une procédure de randomisation par blocs de permutation de taille 4 stratifiée sur le centre, permettant rapidement au clinicien de deviner dans quel groupe un patient sera randomisé. Cela peut aussi parfois servir s’il y a eu un biais d’attrition différentiel. L’ajustement peut, dans une certaine mesure, rectifier le biais.
Que perd-on ?
L’ajustement dans les essais cliniques randomisés n’est pas dénué de risques. Même si les essais cliniques sont très souvent enregistrés dans des bases de données comme ClinicalTrials ou EudraCT, le résumé de protocole disponible précise le critère de jugement mais rarement l’analyse statistique. Les protocoles complets détaillant l’analyse statistique ne sont pas toujours disponibles. Si le protocole complet n’est pas disponible les ajustements peuvent être un facteur conscient ou inconscient de P-hacking. Il est fréquent de lancer un très grand nombre d’analyses de sensibilité dans les rapports d’analyse statistique et l’analyse qui permettra le passage du petit p en dessous de 0.05 risque d’être choisie comme analyse principale.
Même un protocole détaillant la méthode, laisse généralement des degrés de liberté.
Exemple : l’analyse principale sera faite en intention de traiter modifiée (exclusion des sujets randomisés sortis d’étude ou décédés avant d’avoir reçu la 1ère cure de traitement) et sera réalisée dans un modèle de Cox expliquant la survie sans progression ajustée sur le centre, l’âge, le Karnofsky, le stade tumoral et le type histologique. Les sujets perdus de vue seront censurés à la date des dernières nouvelles. Le hazard ratio de l’effet traitement sera comparé à la valeur 1 par un test bilatéral au seuil de significativité 5%.
Cela semble clair et précis, mais il manque un grand nombre de détails :
- Par quelle méthode les ex-aequo seront-ils gérés : Efron, Breslow ou méthode exacte ?
- Certains ajustements sont-ils réalisés par stratification (modèle de Cox conditionnel) ? Cela est parfois fait pour l’effet centre.
- Le petit p est-il calculé par le test du rapport de vraisemblance, celui du score ou celui de Wald, ou encore un autre estimateur ?
- Comment seront gérées les données manquantes sur les covariables, notamment le Karnofsky ?
- Comment seront recodées les variables. L’âge, par exemple, peut être introduit sous forme d’une unique variable quantitative (effet log-linéaire), sous forme de polynôme, ou découpé en catégories à seuils prédéfinis (p.e. 18-60, 60-75, >75 ans) ou découpé en quantiles (quintiles, quartiles, tertiles).
- Quel est le niveau de détail du stade ? Distingue-t-on le stade IIa du stade IIb ou regroupe-t-on ces deux modalités en stade II ?
- Quel est le niveau de détail du type histologique ? En effet, on peut toujours sous-typer très précisément avec la biologie moléculaire, ou pas…
- La variable de stade fait-elle référence au cTNM, au pTNM ? Est-ce le stade pré-traitement ou post-traitement néo-adjuvant ?
- Comment sont gérées les valeurs aberrantes dans les covariables découvertes après le lever d’aveugle ?
- Quelles conditions de validité seront testées ? Y aura-t-il des tests d’interaction ? Si oui, que fera-t-on si certains sont significatifs ?
Pour l’item 10, la réponse évidente (de mon point de vue), est la non prise en compte des interactions, mais il n’est pas sûr que ce soit le comportement de tous les statisticiens. De même, pour l’item 9, la réponse évidente est l’imputation de la valeur aberrante par la même méthode de gestion des données manquantes que les autres, évitant ainsi un biais de classement différentiel, mais j’ai souvent observé dans ma pratique de biostatisticien, le comportement correspondant à « corriger » la donnée à partir du dossier médical, en gardant la trace de la modification dans le script d’analyse.
En analyse non ajustée, il existe déjà un espace de liberté permettant du P-hacking (p.e. plusieurs estimateurs existent, la gestion des ex-aequo se pose toujours), mais ces possibilités explosent complètement en cas d’analyse ajustée. Enfin, il est toujours possible de ne pas respecter du tout le protocole, sans que ce soit pour autant visible dans l’article. J’ai déjà observé un essai clinique randomisé dont les résultats sont publiés dans le Lancet pour lequel le protocole spécifiait que l’analyse principale serait faite dans une régression logistique ajustée sur la sévérité de la maladie à baseline et d’autres variables qui ressortiraient dans l’analyse univariée. Au final, plusieurs techniques de pas-à-pas ont été utilisées et l’article a été publié avec un modèle log-binomial non ajusté sur la sévérité de la maladie à baseline mais ajusté sur un score clinique à baseline qui était ressorti dans les analyses pas-à-pas (basées sur la P-valeur puis sur l’AIC). Cet exemple ne prouve pas que ces écarts au protocole sont fréquents, mais qu’ils sont possibles. Comme le protocole n’a pas été publié, cela est invisible.
Au delà du P-hacking conscient ou inconscient, il existe le risque d’erreur d’analyse. La manipulation des outils statistiques n’est pas évidente et il est toujours possible de se tromper dans la programmation d’une imputation, d’un recodage de variable ou de l’estimation d’un modèle. Plus le nombre de variables impliquées est grand et plus le risque d’erreur est, a priori, élevé. Je ne dispose pas de données à ce jour pour évaluer la fréquence ou l’ampleur de ce problème.
Il apparaît aussi le problème du choix du modèle, pour lequel il est aisé de faire le mauvais choix. Sur un critère de jugement binaire, appliquera-t-on un modèle de régression logistique (logit-binomial), un modèle log-binomial, un modèle identité-binomial ou un modèle linéaire gaussien ? Si on ajuste sur l’effet centre, va-t-on utiliser les équations d’estimation généralisées (GEE), un modèle linéaire généralisé à effets mixtes (GLMM) ou un modèle linéaire généralisé à effet fixe ? Le problème, c’est que l’analyse univariée fournira aisément un résultat pertinent, alors que peu des modèles sus-cités fournissent des résultats aussi robustes. Une régression logistique fournit un odds ratio conditionnel ininterprétable dans un GLMM car conditionnel à des variables inobservables. Une régression logistique ou un modèle log-binomial fournit un odds ratio conditionnel rarement converti en effet marginal. Comme vu au-dessus, il est « gonflé » par rapport à l’effet marginal. Ensuite, la régression logistique comme la log-binomiale fournissent des statistiques relatives (odds ratio ou rapports de proportions) qui reflètent bien mal le bénéfice réel du traitement dans un essai clinique randomisé. En effet, un risque relatif à 0.80 sur un risque touchant la moitié des sujets correspond à une réduction de 10% du risque absolu, soit seulement 10 sujets à traiter pour éviter un événement. Par contre, le même risque relatif appliqué à un risque extrêmement rare tel que 0.1%, obligera à traiter 5000 personnes pour éviter un événement. C’est pour cela, par exemple, qu’une antibioproxphylaxie dans des chirurgies à très haut risque infectieux se justifie alors qu’elle serait futile dans des opérations à très bas risque.
Le modèle identité-binomial semble pertinent, évaluant directement une différence absolue de risque, mais celui-ci montre ses limites lorsque des interactions apparaissent dans le modèle. Comment estimer le bénéfice net d’un traitement lorsque la différence absolue de risque diffère selon le sous-groupe ? En présence d’une interaction quantitative, c’est l’effet marginal qui nous permet d’évaluer le bénéfice net. Si 10% des sujets (mauvais pronostic) voient leur risque d’évolution défavorable baisser de 30% alors que 90% des sujets (bon pronostic) voient leur risque d’évolution défavorable baisser de 20% alors en donnant le traitement innovant à l’ensemble des sujets ont réduit de 0.10×0.30 + 0.90×0.20 = 21%. Un modèle linéaire non ajusté estimera, sans biais, les 21% de bénéfice. Un modèle linéaire gaussien ajusté estimera aussi, sans biais, les 21% de bénéfice car l’homoscédasticité supposée par le modèle conduira à une statistique ajustée égale à la des sous-groupes pondérée par l’effectif du sous-groupe. Cela est une propriété de la méthode d’estimation des moindres carrés. Le modèle identité-binomial, par contre, supposera que la variance est plus faible pour les pourcentages proches de 0% ou de 100% et donnera donc un poids plus fort au sous-groupe correspondant. En caricaturant volontairement, si la population est composée d’un groupe de 80% de patients ayant un risque à 99% (réduit de à 89% par le traitement, soit -10%) et 20% de patients ayant un risque à 50% (réduit à 49% par le traitement, soit -1%), alors le modèle identité-binomial ajusté sur le facteur pronostique estimera le bénéfice du traitement à -6.2% (espérance de l’estimateur) contre -2.8% pour un modèle identité-binomial non ajusté ou un modèle linéaire gaussien ajusté ou non ajusté. Le vrai bénéfice, si on donne le traitement à tout le monde, correspond à cette seconde estimation.
Il est illusoire de penser que les interactions quantitatives n’existent pas. Déjà, par principe, s’il n’existe pas d’interaction quantitative dans un modèle logistique, alors il en existera dans le modèle linéaire et vice versa. Les deux modèles sont fondamentalement contradictoires (sauf s’ils contiennent tous deux tous les termes d’interactions possibles). Les autres modèles sont aussi contradictoires : log-binomial, probit, etc. La stratégie consistant à tester les interactions et à accepter l’hypothèse nulle d’absence d’interaction par défaut de preuve du contraire, serait inepte à un bayésien qui sait que la probabilité a priori d’interaction est à peu près égale à 100%. C’est pourquoi, il est préférable de construire des statistiques « robustes » aux interactions quantitatives. Pour cela, il est possible d’utiliser un modèle linéaire gaussien ou identité-binomial non ajusté ou un modèle linéaire gaussien ajusté. Il est aussi possible de se baser sur un modèle AVEC interactions dès le départ, puis de reconstruire la statistique marginale en calculant la moyenne des effets dans chacun des sous-groupe pondérée par la taille du sous-groupe. Comme la covariance entre les sous-groupes devient nulle lorsqu’on utilise un modèle avec des interactions complètes, le calcul n’est pas super compliqué. Le choix du modèle n’a alors plus d’importance puisqu’on estime directement les effets moyens en sous-groupes. En présence de variable pronostique quantitative, il n’y a pas de solution de codage parfaite parce qu’on ne peut pas modéliser la nature de la relation de manière exacte. Le problème disparaît si on n’ajuste pas du tout ou si on découpe la variable quantitative en tranches (ajustement partiel).
En cas d’interaction qualitative, les problèmes décrits ci-dessus sont exacerbés. C’est probablement un phénomène rare, heureusement, mais il est préférable de se comporter aussi bien que possible s’il advenait. Dans le cas d’une interaction qualitative, le modèle identité-binomial est susceptible de montrer un effet opposé à l’effet marginal réel ! Les interactions qualitatives sont problématiques dans tous les cas parce que le traitement est bénéfique à un sous-groupe identifiable de patients alors qu’il est nocif à un autre sous-groupe identifiable de patients. Malheureusement, la puissance statistique nécessaire à la détection de ce phénomène est loin d’être satisfaisante dans la plupart des études. Cela est d’autant plus vrai que les sous-groupes sont déséquilibrés. C’est pourquoi on évitera, dès le départ, par des critères d’inclusion judicieux, d’avoir une population trop hétérogène avec une probabilité d’interaction forte. Cela justifie, par exemple, qu’on évite de mélanger des enfants et des adultes dans les évaluations de traitements psychiatriques. Néanmoins, dans le cas où on se fait avoir, c’est-à-dire, où il existe une interaction qualitative sur une variable qu’on n’avait pas anticipé et pour laquelle la puissance est totalement insuffisante pour retrouver une tendance dans une analyse en sous-groupes, alors on devra « vivre » avec et donner le traitement innovant à tout le monde. C’est la même chose avec les variables d’interaction inconnues (p.e. dosage biologique encore inconnu) : en l’absence de connaissance, on évalue le bénéfice global. C’est là que l’effet marginal directement estimé par le modèle linéaire gaussien reflètera le bénéfice pragmatique. Empiriquement, il semblerait que le modèle de régression logistique ne puisse pas conduire à l’erreur de 3ème espèce (effet significatif dans le sens opposé à l’effet réel) là où le probit-binomial, l’identité-binomial et le log-binomial peuvent. Il semblerait qu’en présence d’interaction, même si elle n’est pas prise en compte dans le modèle logistique, l’effet marginal prédit par le modèle logistique est correct (identique au modèle linéaire ou au modèle non ajusté) dans le cas d’un ajustement sur une covariable catégorielle.
Il existe aussi le problème de non convergence très fréquent dans le modèle log-binomial lorsqu’on ajuste sur une variable quantitative ou sur de nombreuses variables binaires. Cela est dû au fait que le modèle est grossièrement faux, conduisant à des prédictions dépassant le risque de 1. Il y a de nombreuses interactions quantitatives ou défauts de log-linéarité dans ces modèles et comme vu au-dessus, il n’est plus possible d’estimer un effet conditionnel ou marginal de manière fiable. Par ailleurs, que faire en cas de non convergence ? Fournir un effet non ajusté ? Cela paraît raisonnable, mais la procédure en deux étapes entraîne une erreur statistique mal caractérisée. C’est par exemple, lorsque l’effet d’une covariable est surestimé, que le défaut de convergence apparaît, et dans ce cas précis, on supprime l’ajustement, supposant forçant son effet est à zéro et créant une fluctuation d’échantillonnage discrète sur la statistique principale. En bref, en ajoutant un seul sujet, on peut changer l’estimation principale de manière principale. Sous l’hypothèse d’absence d’effet de la variable principale, cela entraîne une erreur mais pas un biais car ça n’a aucune raison d’avantager un groupe que l’autre. Sous l’hypothèse d’existence d’un effet, cela pourrait peut-être engendrer un biais minime, car il y a à peu près une chance sur deux que cela fasse fluctuer la statistique principale dans un sens et une chance sur deux que ça la fasse fluctuer dans l’autre étant donné que la corrélation entre la covariable et la variable principale est totalement aléatoire de moyenne que la variable
Il existe aussi le problème de non convergence très fréquent dans le modèle log-binomial lorsqu’on ajuste sur une variable quantitative ou sur de nombreuses variables binaires. Cela est dû au fait que le modèle est grossièrement faux, conduisant à des prédictions dépassant le risque de 1. Il y a de nombreuses interactions quantitatives ou défauts de log-linéarité dans ces modèles et comme vu au-dessus, il n’est plus possible d’estimer un effet conditionnel ou marginal de manière fiable. Par ailleurs, que faire en cas de non convergence ? Fournir un effet non ajusté ? Cela paraît raisonnable, mais la procédure en deux étapes entraîne une erreur statistique mal caractérisée. C’est par exemple, lorsque l’effet d’une covariable est surestimé, que le défaut de convergence apparaît, et dans ce cas précis, on supprime l’ajustement, supposant forçant son effet est à zéro et créant une fluctuation d’échantillonnage discrète sur la statistique principale. En bref, en ajoutant un seul sujet, on peut changer l’estimation principale de manière principale. Sous l’hypothèse d’absence d’effet de la variable principale, cela entraîne une erreur mais pas un biais car ça n’a aucune raison d’avantager un groupe que l’autre. Sous l’hypothèse d’existence d’un effet, cela pourrait peut-être engendrer un biais minime, car il y a à peu près une chance sur deux que cela fasse fluctuer la statistique principale dans un sens et une chance sur deux que ça la fasse fluctuer dans l’autre étant donné que la corrélation entre la covariable et la variable principale est totalement aléatoire et d’espérance nulle. Difficile de dire si l’erreur aléatoire augmente un peu le risque alpha ou le diminue un peu. En tout cas, l’erreur aléatoire ne suit pas une loi normale.
Une autre option, en cas de non-convergence d’un modèle log-binomial, c’est d’utiliser un modèle tout autre à ce moment là, tel qu’un modèle logistique. Cela est problématique parce que la statistique fournie n’est plus comparable. Les fluctuations d’échantillonnage fréquentistes deviennent presque ininterprétables puisque la base de la statistique fréquentiste, c’est qu’un même protocole conduit à une même statistique.
Le modèle identité-binomial a des défauts de convergence aussi, même s’ils sont beaucoup plus rares que dans le modèle log-binomial. L’usage d’un modèle linéaire gaussien avec des ajustements parcimonieux (une ou deux variables pronostiques majeures, les autres étant généralement futiles) évite le problème.
Le problème de non-convergence est aussi une problématique à prendre en compte dans le protocole, qui doit préciser l’usage de modèles de secours. Autrement, cela pourrait être un facteur de P-hacking ou de non reproductibilité des analyses.
Synthèse
Nous avons vu qu’un ajustement statistique dans un essai clinique randomisé permet de recruter 5% de patients en moins en cas de facteur pronostic important et que ce chiffre peut monter jusqu’à 10% dans les conditions ou un facteur pronostic absolument majeur existe (en mélangeant les stades I à III du cancer du colon dans un même essai clinique par exemple). Il existe aussi un bénéfice de rectification des biais dû à une étude mal conduite, telle qu’une triche avec la randomisation.
Par contre, l’ajustement pose des problèmes de P-hacking et a de nombreuses limites d’interprétation à moins qu’il ne soit réalisé de manière très rigoureuse:
- Précision exacte de la méthode de traitement des données manquantes des covariables
- Précision du paramétrage exact du modèle, tel que l’estimateur
- Précision du codage exact des covariables rentrées dans le modèle
- Usage d’un modèle linéaire gaussien pour une variable binaire plutôt que les régressions logistiques, log-binomiales ou identité-binomiales
- Publication du protocole avec le plan d’analyse statistique le plus tôt possible !
Cela est plus facile à réaliser si vous ajustez sur peu de covariables et vous concentrez seulement sur une ou deux covariables pronostiques majeures, pour laquelle la qualité de la donnée est bonne (donnée de routine bien renseignée). S’il y a plusieurs covariables, ajoutez les termes d’interaction afin d’éviter les problèmes de fausses hypothèses.
Si vous êtes méthodologiste, je vous invite à être extrêmement explicite dans le protocole même pour un modèle non ajusté. Je vous conseille de ne faire un ajustement qu’à condition (i) de vous assurer que le protocole sera publié et (ii) qu’il existe un facteur pronostique majeur.
Si vous lisez un article, je vous conseille de toujours essayer d’obtenir le protocole, et de vérifier, s’il existe, qu’il a été respecté, notamment sur le choix du critère de jugement principal et le choix de l’analyse principale. Si le protocole n’est pas publié ou qu’il est incomplet, méfiez vous des analyses ajustées.
Laisser un commentaire